TOC PREV NEXT INDEX

Put your logo here!

4.6 Multidimensional Arrays

The 80x86 hardware can easily handle single dimension arrays. Unfortunately, there is no magic addressing mode that lets you easily access elements of multidimensional arrays. That's going to take some work and lots of instructions.

Before discussing how to declare or access multidimensional arrays, it would be a good idea to figure out how to implement them in memory. The first problem is to figure out how to store a multi-dimensional object into a one-dimensional memory space.

Consider for a moment a Pascal array of the form "A:array[0..3,0..3] of char;". This array contains 16 bytes organized as four rows of four characters. Somehow you've got to draw a correspondence with each of the 16 bytes in this array and 16 contiguous bytes in main memory. Figure 4.2 shows one way to do this:



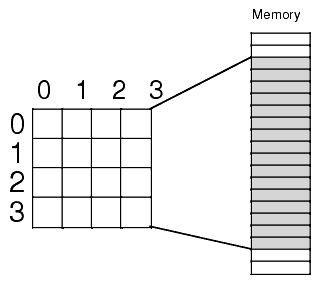
Figure 4.2 Mapping a 4x4 Array to Sequential Memory Locations

The actual mapping is not important as long as two things occur: (1) each element maps to a unique memory location (that is, no two entries in the array occupy the same memory locations) and (2) the mapping is consistent. That is, a given element in the array always maps to the same memory location. So what you really need is a function with two input parameters (row and column) that produces an offset into a linear array of sixteen memory locations.

Now any function that satisfies the above constraints will work fine. Indeed, you could randomly choose a mapping as long as it was unique. However, what you really want is a mapping that is efficient to compute at run time and works for any size array (not just 4x4 or even limited to two dimensions). While there are a large number of possible functions that fit this bill, there are two functions in particular that most programmers and most high level languages use: row major ordering and column major ordering.

4.6.1 Row Major Ordering

Row major ordering assigns successive elements, moving across the rows and then down the columns, to successive memory locations. This mapping is demonstrated in Figure 4.3:



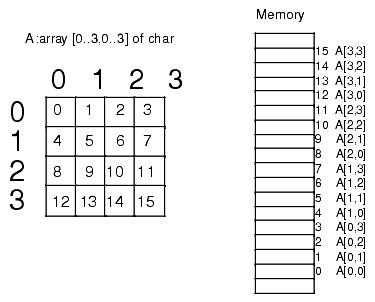
Figure 4.3 Row Major Array Element Ordering

Row major ordering is the method employed by most high level programming languages including Pascal, C/C++, Java, Ada, Modula-2, etc. It is very easy to implement and easy to use in machine language. The conversion from a two-dimensional structure to a linear array is very intuitive. You start with the first row (row number zero) and then concatenate the second row to its end. You then concatenate the third row to the end of the list, then the fourth row, etc. (see Figure 4.4).



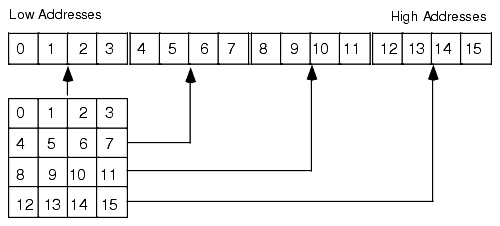
Figure 4.4 Another View of Row-Major Ordering for a 4x4 Array

For those who like to think in terms of program code, the following nested Pascal loop also demonstrates how row major ordering works: 

index := 0;
 
for colindex := 0 to 3 do
 
	for rowindex := 0 to 3 do 
 
	begin
 

		memory [index] := rowmajor [colindex][rowindex];
 
		index := index + 1;
 
	end;

The important thing to note from this code, that applies regardless of the number of dimensions, is that the rightmost index increases the fastest. That is, as you allocate successive memory locations you increment the rightmost index until you reach the end of the current row. Upon reaching the end, you reset the index back to the beginning of the row and increment the next successive index by one (that is, move down to the next row.). This works equally well for any number of dimensions1. The following Pascal segment demonstrates row major organization for a 4x4x4 array: 

index := 0;
 
for depthindex := 0 to 3 do
 
	for colindex := 0 to 3 do
 
	   for rowindex := 0 to 3 do begin
 

		memory [index] := rowmajor [depthindex][colindex][rowindex];
 
		index := index + 1;
 

	   end;

The actual function that converts a list of index values into an offset doesn't involve loops or much in the way of fancy computations. Indeed, it's a slight modification of the formula for computing the address of an element of a single dimension array. The formula to compute the offset for a two-dimension row major ordered array declared in Pascal as "A:array [0..3,0..3] of integer" is 

Element_Address = Base_Address + (colindex * row_size + rowindex) * Element_Size

As usual, Base_Address is the address of the first element of the array (A[0][0] in this case) and Element_Size is the size of an individual element of the array, in bytes. Colindex is the leftmost index, rowindex is the rightmost index into the array. Row_size is the number of elements in one row of the array (four, in this case, since each row has four elements). Assuming  Element_Size is one, this formula computes the following offsets from the base address: 

	Column			Row			Offset into Array
 
	index			Index
 
	0			0			0
 
	0			1			1
 
	0			2			2
 
	0			3			3
 
	1			0			4
 
	1			1			5
 
	1			2			6
 
	1			3			7
 
	2			0			8
 
	2			1			9
 
	2			2			10
 
	2			3			11
 
	3			0			12
 
	3			1			13
 
	3			2			14
 
	3			3			15

For a three-dimensional array, the formula to compute the offset into memory is the following: 

Address = Base + ((depthindex*col_size+colindex) * row_size + rowindex) * Element_Size

Col_size is the number of items in a column, row_size is the number of items in a row. In C/C++, if you've declared the array as "type A[i] [j] [k];" then row_size is equal to k and col_size is equal to j.

For a four dimensional array, declared in C/C++ as "type A[i] [j] [k] [m];" the formula for computing the address of an array element is 

Address = 
 
Base + (((LeftIndex * depth_size + depthindex)*col_size+colindex) * row_size + 
rowindex) * Element_Size

Depth_size is equal to j, col_size is equal to k, and row_size is equal to m.  LeftIndex represents the value of the leftmost index.

By now you're probably beginning to see a pattern. There is a generic formula that will compute the offset into memory for an array with any number of dimensions, however, you'll rarely use more than four.

Another convenient way to think of row major arrays is as arrays of arrays. Consider the following single dimension Pascal array definition: 

A: array [0..3] of  sometype;

Assume that sometype is the type "sometype = array [0..3] of char;".

A is a single dimension array. Its individual elements happen to be arrays, but you can safely ignore that for the time being. The formula to compute the address of an element of a single dimension array is 

Element_Address = Base + Index * Element_Size

In this case Element_Size happens to be four since each element of A is an array of four characters. So what does this formula compute? It computes the base address of each row in this 4x4 array of characters (see Figure 4.5):



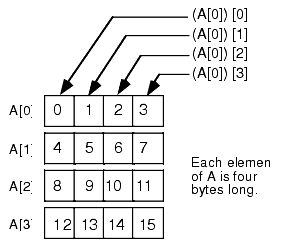
Figure 4.5 Viewing a 4x4 Array as an Array of Arrays

Of course, once you compute the base address of a row, you can reapply the single dimension formula to get the address of a particular element. While this doesn't affect the computation at all, conceptually it's probably a little easier to deal with several single dimension computations rather than a complex multidimensional array element address computation.

Consider a Pascal array defined as "A:array [0..3] [0..3] [0..3] [0..3] [0..3] of char;" You can view this five-dimension array as a single dimension array of arrays. The following Pascal code demonstrates such a definition: 

type
 
		OneD = array [0..3] of char;
 
		TwoD = array [0..3] of OneD;
 
		ThreeD = array [0..3] of TwoD;
 
		FourD = array [0..3] of ThreeD;
 
var
 
		A : array [0..3] of FourD;

The size of OneD is four bytes. Since TwoD contains four OneD arrays, its size is 16 bytes. Likewise, ThreeD is four TwoDs, so it is 64 bytes long. Finally, FourD is four ThreeDs, so it is 256 bytes long. To compute the address of "A [b, c, d, e, f]" you could use the following steps:

Not only is this scheme easier to deal with than the fancy formulae given earlier, but it is easier to compute (using a single loop) as well. Suppose you have two arrays initialized as follows

A1 = [256, 64, 16, 4, 1] and A2 = [b, c, d, e, f]

then the Pascal code to perform the element address computation becomes: 

		for i := 0 to 4 do
 
			base := base + A1[i] * A2[i];

Presumably base contains the base address of the array before executing this loop. Note that you can easily extend this code to any number of dimensions by simply initializing A1 and A2 appropriately and changing the ending value of the for loop.

As it turns out, the computational overhead for a loop like this is too great to consider in practice. You would only use an algorithm like this if you needed to be able to specify the number of dimensions at run time. Indeed, one of the main reasons you won't find higher dimension arrays in assembly language is that assembly language displays the inefficiencies associated with such access. It's easy to enter something like "A [b,c,d,e,f]" into a Pascal program, not realizing what the compiler is doing with the code. Assembly language programmers are not so cavalier - they see the mess you wind up with when you use higher dimension arrays. Indeed, good assembly language programmers try to avoid two dimension arrays and often resort to tricks in order to access data in such an array when its use becomes absolutely mandatory. But more on that a little later.

4.6.2 Column Major Ordering

Column major ordering is the other function frequently used to compute the address of an array element. FORTRAN and various dialects of BASIC (e.g., older versions of Microsoft BASIC) use this method to index arrays.

In row major ordering the rightmost index increased the fastest as you moved through consecutive memory locations. In column major ordering the leftmost index increases the fastest. Pictorially, a column major ordered array is organized as shown in Figure 4.6:



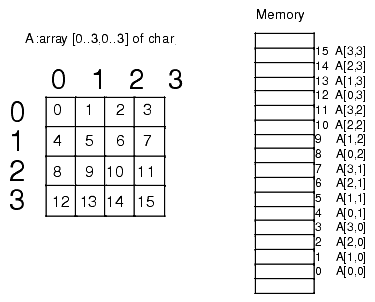
Figure 4.6 Column Major Array Element Ordering

The formulae for computing the address of an array element when using column major ordering is very similar to that for row major ordering. You simply reverse the indexes and sizes in the computation:

For a two-dimension column major array: 

Element_Address = Base_Address + (rowindex * col_size + colindex) * Element_Size

For a three-dimension column major array: 

Address = Base + ((rowindex*col_size+colindex) * depth_size + depthindex) * 
Element_Size

For a four-dimension column major array: 

Address = 
 
	Base + (((rowindex * col_size + colindex)*depth_size + depthindex) * 
 
		Left_size + Leftindex) * Element_Size

The single Pascal loop provided for row major access remains unchanged (to access A[b][c][d][e][f]): 

		for i := 0 to 4 do
 
			base := base + A1[i] * A2[i];

Likewise, the initial values of the A1 array remain unchanged: 

	A1 = {256, 64, 16, 4, 1}

The only thing that needs to change is the initial values for the A2 array, and all you have to do here is reverse the order of the indices: 

	A2 = {f, e, d, c, b}

4.7 Allocating Storage for Multidimensional Arrays

If you have an m x n array, it will have m * n elements and require m*n*Element_Size bytes of storage. To allocate storage for an array you must reserve this amount of memory. As usual, there are several different ways of accomplishing this task. Fortunately, HLA's array declaration syntax is very similar to high level language array declaration syntax, so C/C++, BASIC, and Pascal programmers will feel right at home. To declare a multidimensional array in HLA, you use a declaration like the following: 

		ArrayName: elementType [ comma_separated_list_of_dimension_bounds ];

For example, here is a declaration for a 4x4 array of characters: 

GameGrid: char[ 4, 4 ];

Here is another example that shows how to declare a three dimensional array of strings: 

NameItems: string[ 2, 3, 3 ];

Remember, string objects are really pointers, so this array declaration reserves storage for 18 double word pointers (2*3*3=18).

As was the case with single dimension arrays, you may initialize every element of the array to a specific value by following the declaration with the assignment operator and an array constant. Array constants ignore dimension information; all that matters is that the number of elements in the array constant correspond to the number of elements in the actual array. The following example shows the GameGrid declaration with an initializer: 

	GameGrid: char[ 4, 4 ] := 
 
		[ 
 
			`a', `b', `c', `d',
 
			`e', `f', `g', `h',
 
			`i', `j', `k', `l',
 
			`m', `n', `o', `p'
 
		];

Note that HLA ignores the indentation and extra whitespace characters (e.g., newlines) appearing in this declaration. It was laid out to enhance readability (which is always a good idea). HLA does not interpret the four separate lines as representing rows of data in the array. Humans do, which is why it's good to lay out the initial data in this manner, but HLA completely ignores the physical layout of the declaration. All that matters is that there are 16 (4*4) characters in the array constant. You'll probably agree that this is much easier to read than 

	GameGrid: char[ 4,4 ] := 
 
		[ `a', `b', `c', `d', `e', `f', `g', `h', `i', `j', `k', `l', `m',
 
		  `n', `o', `p' ];

Of course, if you have a large array, an array with really large rows, or an array with many dimensions, there is little hope for winding up with something reasonable. That's when comments that carefully explain everything come in handy.

As with single dimension arrays, you can use the DUP operator to initialize each element of a really large array with the same value. The following example initializes a 256x64 array of bytes so that each byte contains the value $FF: 

StateValue: byte[ 256, 64 ] := 256*64 dup [$ff];

Note the use of a constant expression to compute the number of array elements rather than simply using the constant 16,384 (256*64). The use of the constant expression more clearly suggests that this code is initializing each element of a 256x64 element array than does the simple literal constant 16,384.

Another HLA trick you can use to improve the readability of your programs is to use nested array constants. The following is an example of an HLA nested array constant: 

[ [0, 1, 2], [3, 4], [10, 11, 12, 13] ]

Whenever HLA encounters an array constant nested inside another array constant, it simply removes the brackets surrounding the nested array constant and treats the whole constant as a single array constant. For example, HLA converts the nested array constant above to the following:

[ 0, 1, 2, 3, 4, 10, 11, 12, 13 ]

You can take advantage of this fact to help make your programs a little more readable. For multidimensional array constants you can enclose each row of the constant in square brackets to denote that the data in each row is grouped and separate from the other rows. As an example, consider the following declaration for the GameGrid array that is identical (as far as HLA is concerned) to the previous declaration: 

	GameGrid: char[ 4, 4 ] := 
 
		[ 
 
			[ `a', `b', `c', `d' ],
 
			[ `e', `f', `g', `h' ],
 
			[ `i', `j', `k', `l' ],
 
			[ `m', `n', `o', `p' ]
 
		];

This declaration makes it clearer that the array constant is a 4x4 array rather than just a 16-element one-dimensional array whose elements wouldn't fit all on one line of source code. Little aesthetic improvements like this are what separate mediocre programmers from good programmers.

4.8 Accessing Multidimensional Array Elements in Assembly Language

Well, you've seen the formulae for computing the address of an array element. You've even looked at some Pascal code you could use to access elements of a multidimensional array. Now it's time to see how to access elements of those arrays using assembly language.

The MOV, SHL, and INTMUL instructions make short work of the various equations that compute offsets into multidimensional arrays. Let's consider a two dimension array first: 


 

 
static
 
	i:		int32;
 
	j:		int32;
 
	TwoD:		int32[ 4, 8 ];
 

		 .
 
		 .
 
		 .
 

// To peform the operation TwoD[i,j] := 5; you'd use code like the following.
 
// Note that the array index computation is (i*8 + j)*4.
 

		mov( i, ebx );
 
		shl( 3, ebx );						// Multiply by eight (shl by 3 is a multiply by 8).
 
		add( j, ebx );
 
		mov( 5, TwoD[ ebx*4 ] );

Note that this code does not require the use of a two register addressing mode on the 80x86. Although an addressing mode like TwoD[ebx][esi] looks like it should be a natural for accessing two dimensional arrays, that isn't the purpose of this addressing mode.

Now consider a second example that uses a three dimension array: 

static
 
	i:			int32;
 
	j:			int32;
 
	k:			int32;
 
	ThreeD:			int32[ 3, 4, 5 ];
 
		.
 
		.
 
		.
 

// To peform the operation ThreeD[i,j,k] := ESI; you'd use the following code
 
// that computes ((i*4 + j)*5 + k )*4 as the address of ThreeD[i,j,k].
 

		mov( i, ebx );
 
		shl( 2, ebx );						// Four elements per column.
 
		add( j, ebx );
 
		intmul( 5, ebx );						// Five elements per row.
 
		add( k, ebx );
 
		mov( esi, ThreeD[ ebx*4 ] );

Note that this code uses the INTMUL instruction to multiply the value in EBX by five. Remember, the SHL instruction can only multiply a register by a power of two. While there are ways to multiply the value in a register by a constant other than a power of two, the INTMUL instruction is more convenient2.

1By the way, the number of dimensions of an array is its arity.

2A full discussion of multiplication by constants other than a power of two appears in the chapter on arithmetic.

Web Site Hits Since
Jan 1, 2000

TOC PREV NEXT INDEX